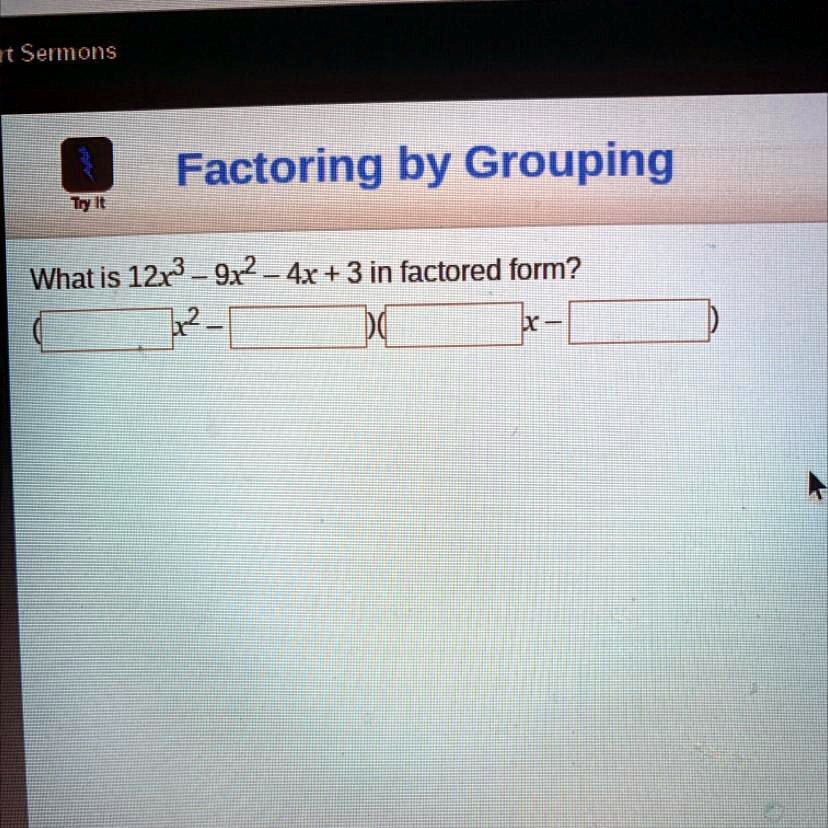
What is
in factored form?
The Correct Answer and Explanation is:
We are asked to factor the polynomial: 12×3−9×2−4x+312x^3 – 9x^2 – 4x + 3
Step-by-step Factoring by Grouping:
1. Group terms:
Group the terms in pairs: (12×3−9×2)+(−4x+3)(12x^3 – 9x^2) + (-4x + 3)
2. Factor out the greatest common factor (GCF) from each group:
From the first group 12×3−9x212x^3 – 9x^2, the GCF is 3x23x^2: 3×2(4x−3)3x^2(4x – 3)
From the second group −4x+3-4x + 3, we factor out −1-1: −1(4x−3)-1(4x – 3)
So we now have: 3×2(4x−3)−1(4x−3)3x^2(4x – 3) – 1(4x – 3)
3. Factor out the common binomial factor (4x−3)(4x – 3): (3×2−1)(4x−3)(3x^2 – 1)(4x – 3)
Final Answer:
(3×2−1)(4x−3)\boxed{(3x^2 – 1)(4x – 3)}
Explanation
Factoring by grouping is a method used to factor polynomials with four terms. It involves grouping terms in pairs, factoring out the greatest common factor from each group, and then factoring out a common binomial factor.
In the polynomial 12×3−9×2−4x+312x^3 – 9x^2 – 4x + 3, we first group the terms: (12×3−9×2)(12x^3 – 9x^2) and (−4x+3)(-4x + 3). These groupings allow us to see a common factor within each pair.
From the first group 12×3−9x212x^3 – 9x^2, the common factor is 3x23x^2. Factoring this gives 3×2(4x−3)3x^2(4x – 3). In the second group −4x+3-4x + 3, we factor out −1-1 to get −1(4x−3)-1(4x – 3).
Now both groups share a common binomial factor (4x−3)(4x – 3), which can be factored out, resulting in (3×2−1)(4x−3)(3x^2 – 1)(4x – 3).
This shows the expression has been successfully factored. You can verify the result by expanding the factored form using the distributive property: (3×2−1)(4x−3)=3×2(4x)−3×2(3)−1(4x)+1(3)=12×3−9×2−4x+3(3x^2 – 1)(4x – 3) = 3x^2(4x) – 3x^2(3) – 1(4x) + 1(3) = 12x^3 – 9x^2 – 4x + 3
which matches the original polynomial. Factoring is a powerful algebraic tool, helping simplify expressions and solve equations more easily.
